
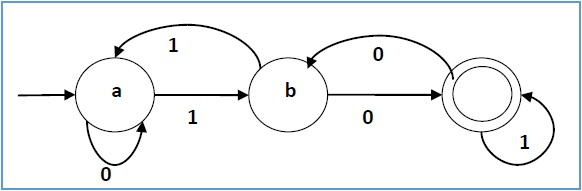
For example, we can look at a deterministic finite automata and immediately know if it can be simplified further- if there exists a smaller DFA that solves the same decision problem. Lots of people are interested in these systems because they’re more tractable: there are more mathematical properties we can assert of the class as a whole. There’s also plenty of systems that are less powerful, aka there are computable decision problems they cannot solve. Conventionally inputs are restricted to binary strings. This branch of math is called formal languages. We have a string of characters and a dictionary that maps single characters to strings: Tag systems are one of my favorite automata, which is easily the third or fourth nerdiest thing I’ve said all month. 4 I wouldn’t be able to explain it well and this wouldn’t be a very informative newsletter. But I don’t think it’s a good demonstration! I used way too many Vim Tricks (tm), like macro/register equivalence, that make understanding how it works really annoying. I’ve already written a Brainfuck interpreter in Vim keystrokes, so I could stop right there and call victory. Esolangs commonly prove their own TCness by implementing a Brainfuck interpreter. BF is TC with only one datatype and eight commands. One of the more popular targets is Brainfuck, an esolang (esoteric language) from the 90s. It’s got too much stuff in it designed for “actually writing real programs” that makes it hard to encode. C is even more of a pain than Turing machines are. If we could write a C interpreter entirely in Vim keystrokes, then we’ve proven that Vim is Turing complete. 3 Instead, the most common way to prove Turing-completeness is to write an interpreter for a system that we already know is Turing-complete, preferably a system that’s more agreeable. Unfortunately Turing machines are a huge pain to work with, so we try to avoid that. The most direct way to prove S is Turing complete by showing that any Turing machine can be converted into an S-construct. 2 We say a model of computation S is Turing-complete if it can solve any problem a Turing machine can, aka S is maximally powerful. Nothing can be more powerful than a Turing machine.
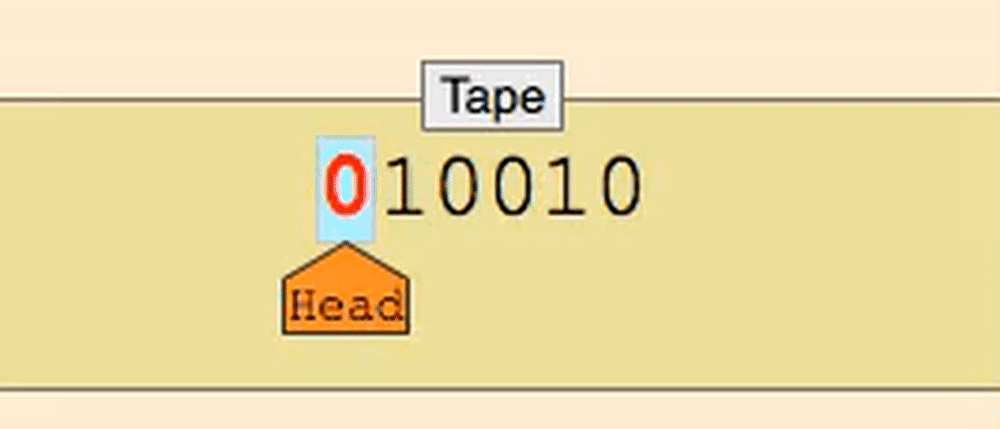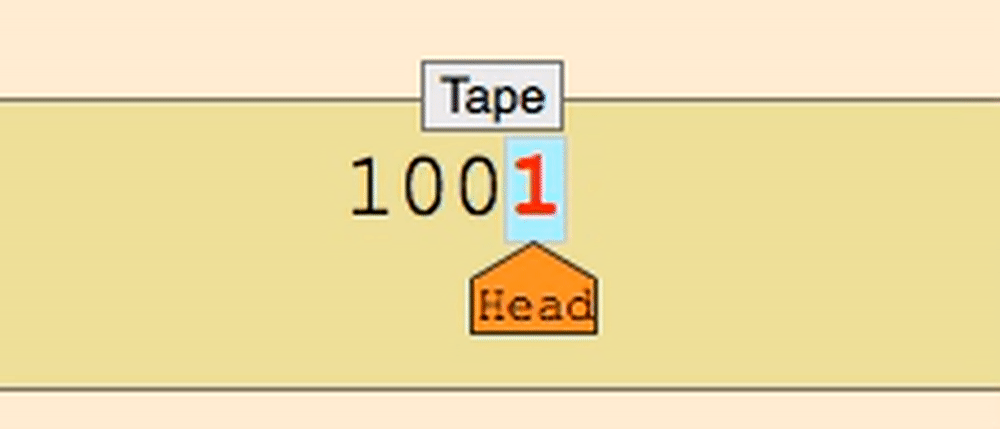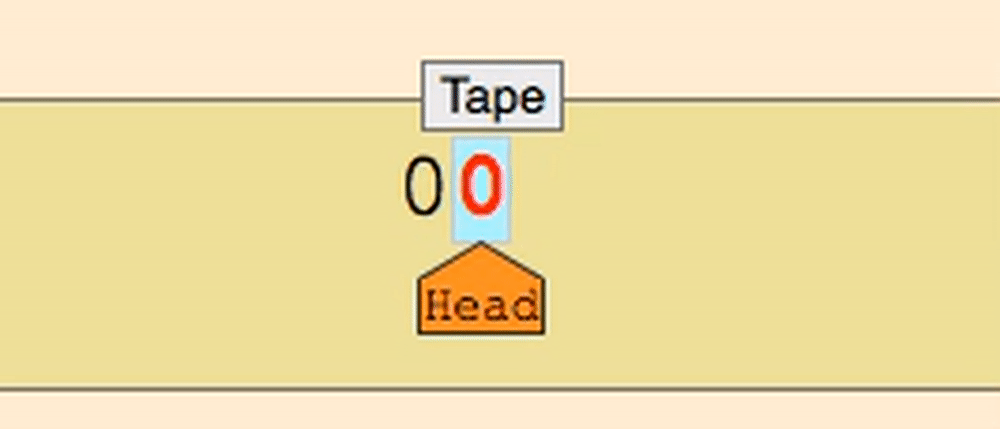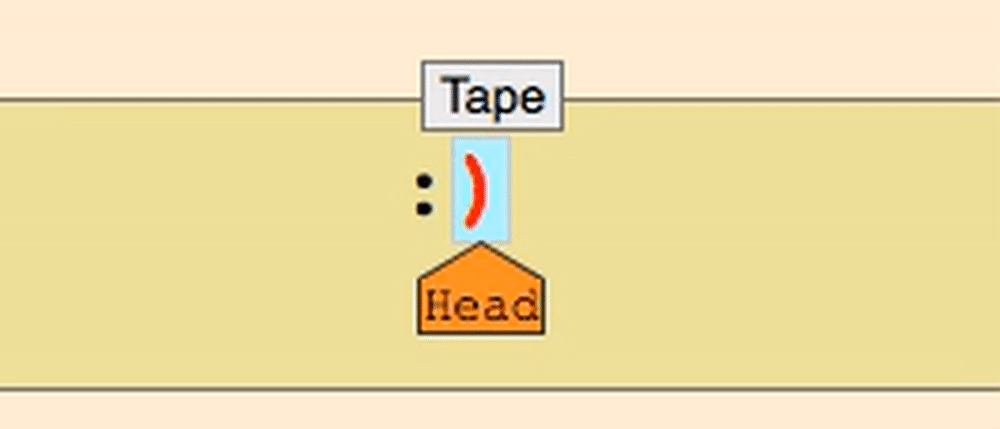
This isn’t formally proven, but it’s empirically held up for a long-ass time.

The Church-Turing Thesis hypothesizes that Turing machines are the upper bound of power: if you cannot implement the algorithm in a Turing machine, you cannot implement the algorithm in any system. One class of “implementation systems” are automata, and a Turing machine is one kind of automata. 1 If we can come up with an algorithm, we can then “implement” it in some mathematical system. We have some predicate P(x) (“x is divisible by 2”, “x contains an A”, etc) and we want to come up with an algorithm that correctly determine P for all possible finite inputs. Very roughly: A decision problem is a standard math problem. I’ll explain how this works, but first, a very brief overview of what I mean by “Turing-complete”.


 0 kommentar(er)
0 kommentar(er)
